Bonjour
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie :
https://computational-dis[...]ts/bohemian-matrices.html
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
exemple ici avec le set {0, 0.2, -i, i}
valeur propre :
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
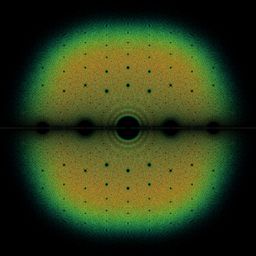
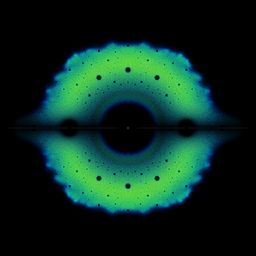
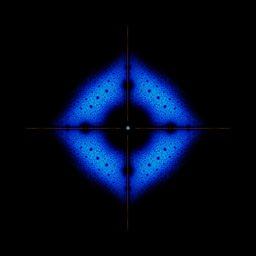
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
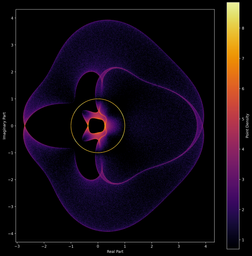
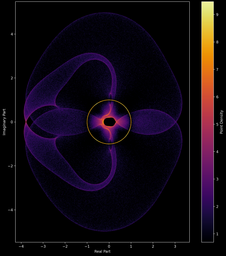
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
Racines complexes de polynômes
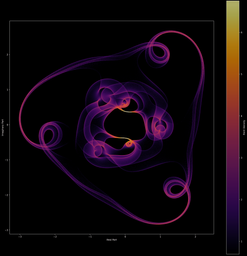
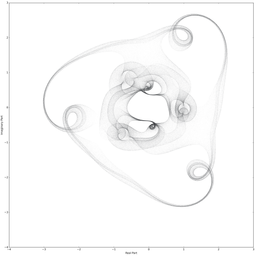
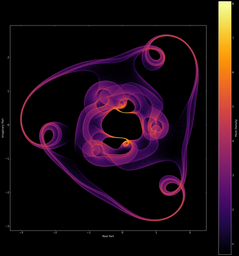
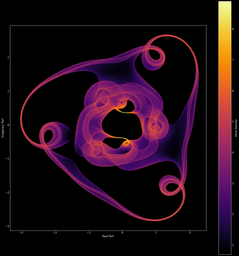
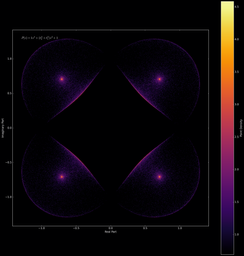
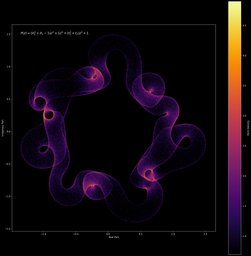
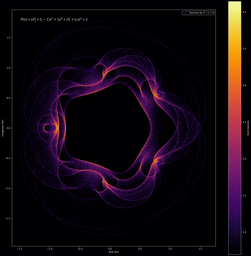
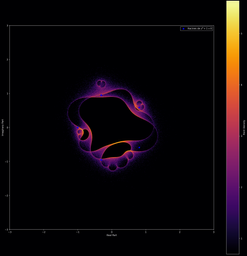
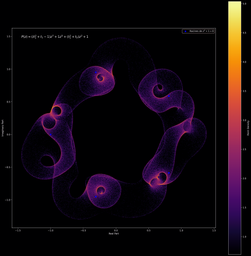
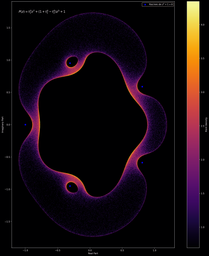
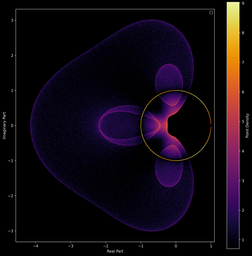
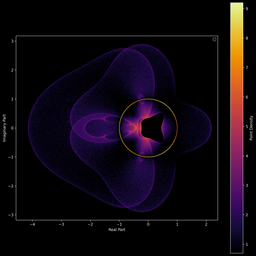
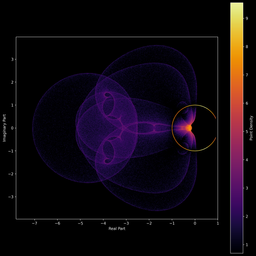
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
https://www.youtube.com/p[...]51VvPVaXEl8A4eycIbaNgfQZK
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
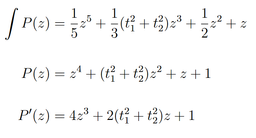
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
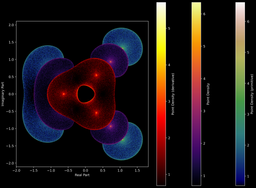
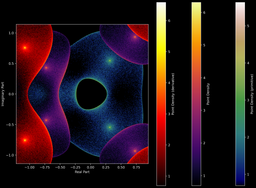
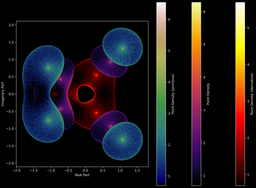
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
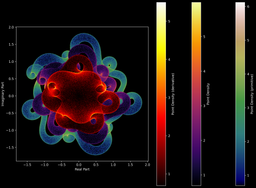
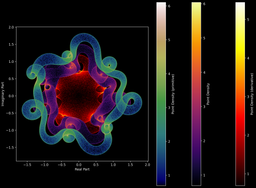
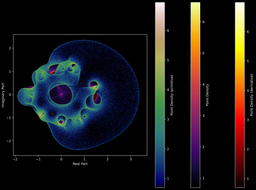
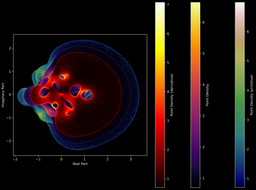
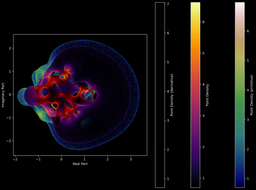
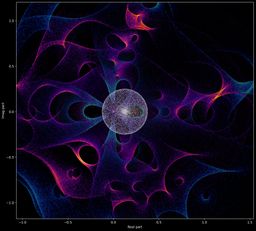
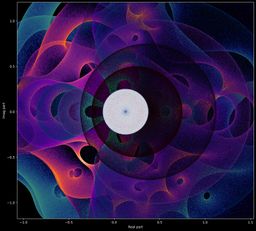
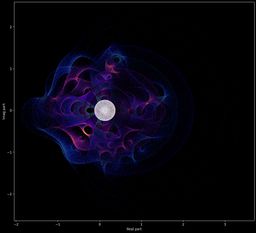
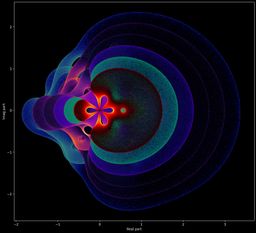
Symétries
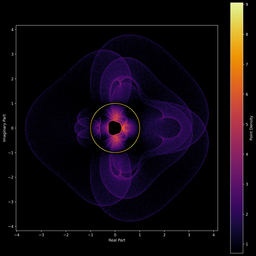
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
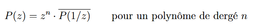
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
À bientôt pour de nouvelles vérités cryptiques, arrachées aux ténèbres insondables de la science où sommeillent les arcanes oubliés de notre univers.
Puissent ces révélations cyclopéennes, sur le mystérieux agencement du spectre des matrices et des racines polynomiales complexe, ouvrir vos esprit aux abîmes du savoir. Que vos intellect effleurent l’Indicible, et sombrent dans les profondeurs abyssales de cette mer de science, inaccessible aux esprits fragiles des yes-life ordinaires.
Pour les esprits en quête de vérités plus profondes, les traces de mes anciens messages demeurent :
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Ou peut-être pas
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie :
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
valeur propre :
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
(note : dans les figures en couleur précédentes, chaque valeur propre correspond à une matrice dont toutes les valeurs appartiennent à un ensemble fixe {a1, a2, a3, ...}. Et pour faire une figure entière, un grand nombres de matrices aléatoires avec des éléments appartenant au set sont générées afin d'obtenir toutes ces valeurs propres complexes.
Alors qu'avec la seconde méthode, il n'y a plus vraiment de set fixié (on choisi juste une matrice et on fait varier aléatoirement certain de ses éléments sur le cercle complexe unité, avec t1 et t2).
Ce sont juste deux méthodes différentes pour faire ces figures de valeurs propres, et les formes produites seront différentes.
On aurait aussi pu regarder le déterminant, ou d'autres propriétés spectrales des matrices pour faire d'autres figures éventuellement.
Racines complexes de polynômes
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
(note: les polynômes sont indiqués sur les images, les variables t1, t2 sont tirées sur le cercle complexe unité)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
À cause de gauss lucas :
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
Symétries
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
Topic Entropie : 
https://onche.org/topic/8[...]t-fonction-de-partition-z
Topic Cactus : https://onche.org/topic/3[...]ooster-de-maniere-sereine
Topic Quantique : https://onche.org/topic/3[...]e-avec-vous-des-questions
Fantastique
J’ai l’impression d’avoir un polynôme dans le cerveau
Osef
Viva New Vegas ! 
Fantastique
mercient
Heu ok , très stylé, post
mercient
"the numbers Mason, what do they mean?"
Bonjour
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie : https://computational-dis[...]ts/bohemian-matrices.html
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
exemple ici avec le set {0, 0.2, -i, i}
valeur propre :
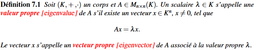
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
Racines complexes de polynômes
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
https://www.youtube.com/p[...]51VvPVaXEl8A4eycIbaNgfQZK
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
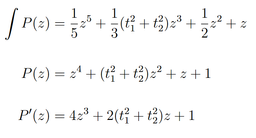
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
Symétries
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
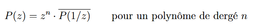
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
À bientôt pour de nouvelles vérités cryptiques, arrachées aux ténèbres insondables de la science où sommeillent les arcanes oubliés de notre univers.
Puissent ces révélations cyclopéennes, sur le mystérieux agencement du spectre des matrices et des racines polynomiales complexe, ouvrir vos esprit aux abîmes du savoir. Que vos intellect effleurent l’Indicible, et sombrent dans les profondeurs abyssales de cette mer de science, inaccessible aux esprits fragiles des yes-life ordinaires.
Pour les esprits en quête de vérités plus profondes, les traces de mes anciens messages demeurent :
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Ou peut-être pas
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie :
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
valeur propre :
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
(note : dans les figures en couleur précédentes, chaque valeur propre correspond à une matrice dont toutes les valeurs appartiennent à un ensemble fixe {a1, a2, a3, ...}. Et pour faire une figure entière, un grand nombres de matrices aléatoires avec des éléments appartenant au set sont générées afin d'obtenir toutes ces valeurs propres complexes.
Alors qu'avec la seconde méthode, il n'y a plus vraiment de set fixié (on choisi juste une matrice et on fait varier aléatoirement certain de ses éléments sur le cercle complexe unité, avec t1 et t2).
Ce sont juste deux méthodes différentes pour faire ces figures de valeurs propres, et les formes produites seront différentes.
On aurait aussi pu regarder le déterminant, ou d'autres propriétés spectrales des matrices pour faire d'autres figures éventuellement.
Racines complexes de polynômes
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
(note: les polynômes sont indiqués sur les images, les variables t1, t2 sont tirées sur le cercle complexe unité)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
À cause de gauss lucas :
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
Symétries
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
Topic Entropie : https://onche.org/topic/8[...]t-fonction-de-partition-z
Topic Cactus : https://onche.org/topic/3[...]ooster-de-maniere-sereine
Topic Quantique : https://onche.org/topic/3[...]e-avec-vous-des-questions
Il n'y a que sur ce forum qu'on peut trouver des pavés de doctorant faits par des mecs qui se nomment PiedJuteux
Je vous aime tous
Tu ne fais pas exception
Bonjour
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie : https://computational-dis[...]ts/bohemian-matrices.html
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
exemple ici avec le set {0, 0.2, -i, i}
valeur propre :
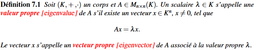
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
Racines complexes de polynômes
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
https://www.youtube.com/p[...]51VvPVaXEl8A4eycIbaNgfQZK
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
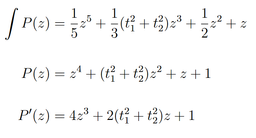
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
Symétries
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
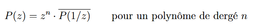
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
À bientôt pour de nouvelles vérités cryptiques, arrachées aux ténèbres insondables de la science où sommeillent les arcanes oubliés de notre univers.
Puissent ces révélations cyclopéennes, sur le mystérieux agencement du spectre des matrices et des racines polynomiales complexe, ouvrir vos esprit aux abîmes du savoir. Que vos intellect effleurent l’Indicible, et sombrent dans les profondeurs abyssales de cette mer de science, inaccessible aux esprits fragiles des yes-life ordinaires.
Pour les esprits en quête de vérités plus profondes, les traces de mes anciens messages demeurent :
Introduction :
Peut-être vous êtes-vous déjà demandé : "tiens, mais à quoi pourrais ressembler la distribution des valeurs propres de matrices bohémiennes dans un plan complexe (2D) ?"
Ou peut-être pas
Quoi qu’il en soit, des gens sur internet ont fait ce travail qui en parle en partie :
Je fais donc ce topic pour présenter le principe, puis étendre cette manière de faire (non pas uniquement à des matrices, mais aussi à des polynômes) afin de voir comment les figures changent en fonction des structures étudiées.
Valeur propres complexes de matrices (bohémienne)
Pour résumer le site mentionné :
matrice bohémienne : une matrice avec des éléments appartenant à un set fini.
valeur propre :
Et voici le type de figures que l’on obtient, en traçant sur le plan complexe les valeurs propres possibles de toutes les matrices bohémiennes existantes pour une certaine dimension et un certain set :
On peut aussi réaliser nos propres figure en s'inspirant de cette méthode et en la modifiant légèrement : on choisit une matrice aux valeurs fixées, puis on décide de faire varier seulement deux valeurs, en les échantillonnant aléatoirement (ici t1 et t2) pour obtenir de jolies figures de valeurs propres.
Mathématiquement :
Les figures correspondent à l’ensemble des valeurs propres complexes obtenues pour chaque échantillonnage de t1 et t2.
Voici un premier essai avec deux valeurs de la matrice qui sont variées suivant une distribution uniforme (avec comme support [-20, 20])
Voici un second essai avec deux valeurs de la matrices qui sont variées suivant une distribution uniforme sur le cercle complexe unité.
(note : dans les figures en couleur précédentes, chaque valeur propre correspond à une matrice dont toutes les valeurs appartiennent à un ensemble fixe {a1, a2, a3, ...}. Et pour faire une figure entière, un grand nombres de matrices aléatoires avec des éléments appartenant au set sont générées afin d'obtenir toutes ces valeurs propres complexes.
Alors qu'avec la seconde méthode, il n'y a plus vraiment de set fixié (on choisi juste une matrice et on fait varier aléatoirement certain de ses éléments sur le cercle complexe unité, avec t1 et t2).
Ce sont juste deux méthodes différentes pour faire ces figures de valeurs propres, et les formes produites seront différentes.
On aurait aussi pu regarder le déterminant, ou d'autres propriétés spectrales des matrices pour faire d'autres figures éventuellement.
Racines complexes de polynômes
Il est aussi possible d’effectuer le même type de figures, mais cette fois avec des polynômes (on remplace juste les valeurs propres complexes par les racines complexes). On peut ainsi obtenir des représentations visuelles de nos polynômes préférés ! (yayy
(note: les polynômes sont indiqués sur les images, les variables t1, t2 sont tirées sur le cercle complexe unité)
Représentation en vidéo
On peut ajouter une troisième variable t3 et la faire évoluer continûment sur le cercle unité.
Pour chaque frame de la vidéo, on trace les racines (ou valeurs propres) pour un grand ensemble de (t1, t2) tirés aléatoirement.
En assemblant les frames, on obtient une animation fluide montrant la transformation progressive de la figure, qui finit par revenir à sa forme initiale après un tour complet.
Playlist complète avec 10 vidéos :
Théorème de Gauss-Lucas
Le théorème de Gauss-Lucas stipule :
Pour un polynôme fixé P(z), les racines de P'(z) se trouvent à l’intérieur de l’enveloppe convexe formée par les racines de P(z).
En superposant sur nos figures les racines de P′(z), on peut visualiser en partie ce résultat. Les points représentant les zéros de la dérivée se regroupent toujours à l’intérieur du domaine formé par les racines originales.
Bon en vrai vu que ce sont des nuages de points (union des racines des polynômes) qui sont tracés ici, on ne peut pas bien visualiser le théorème. Mais on arrive quand même à voir que la coque convexe de ces nuages de points inclut bien les racines de P'(z).
À cause de gauss lucas :
Mainteant, un exemple pour ce polynôme, avec sa primitive et sa dérivée :
On voit bien que les nuages de points des polynômes restent dans l'enveloppe convexe de leur primitive :
Ou bien avec d'autres polynômes et leurs primitives/dérivées :
Symétries
Ces figures révèlent aussi les symétries inhérentes aux polynômes.
Par exemple, un polynôme satisfait une symétrie par rapport au cercle unité s’il vérifie :
Dans ce cas, chaque racine à l’extérieur du cercle unité possède un symétrique par inversion-conjugaison à l’intérieur, ce qui produit des motifs parfaitement réfléchis.
Voilà, c'est tout
Topic Entropie : https://onche.org/topic/8[...]t-fonction-de-partition-z
Topic Cactus : https://onche.org/topic/3[...]ooster-de-maniere-sereine
Topic Quantique : https://onche.org/topic/3[...]e-avec-vous-des-questions
Merci l'auteur pour cette plongée fascinante dans les valeurs propres des matrices bohémiennes (terme que je découvre au passage).
Petite dédicace au joli théorème de Gauss-Lucas, que j'avais traité dans une vidéo youtube.
Petite dédicace au joli théorème de Gauss-Lucas, que j'avais traité dans une vidéo youtube.
Go hp lopax vite
No troll cest un.super topic
No troll cest un.super topic
Pazifieur de choffs - Queer et Patriote - team KJ mignon spé chat
Il n'y a que sur ce forum qu'on peut trouver des pavés de doctorant faits par des mecs qui se nomment PiedJuteux
Et c'est pour cela qu'on l'aime.
Le forum.
Le forum.
Épouse moi
Palu
Vous devez être au niveau
pour voir ce message.
J ai pas tous compris mais jolie pavé + sujet très intéressant
Il y a deux façons de se tromper : L'une est de croire ce qui n'est pas, L'autre de refuser de croire ce qui est
C'était pour une kheyette qui aime les maths à la base, je lui avait envoyé une partie de ce travail en MP
Et c'est pour cela qu'on l'aime.
Le forum.
Le forum.
Et le soir ça parle de feetjob avec un shemale
Je vous aime tous
Tu ne fais pas exception