j'y ai pensé tout à l'heure en plus . . .
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Purée elle prends même plus la peine de me ping correctement car elle sait que je suis sur le topic h24 comme un gros nolife associal contrairement à ce que prétends Oib
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Je suis allée voir où se déroulaient les émeutes à cause de match de foot ( peu importe l’ampleur ) et effectivement c’est surtout Paris et sa banlieue, Marseille, Pays de l’Est et Turquie ( ultra violente la Turquie en plus )
Mais, aussi étonnant que ça puisse paraître, Marseille n’a pas de groupes de hooligans particulièrement connu, si il y’a émeute c’est plus fait par des random contre des hooligans d’autres endroits.
Voici ceux répertoriés par l’équipe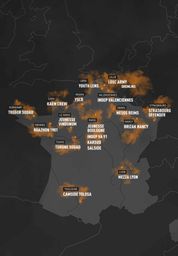
Mais, aussi étonnant que ça puisse paraître, Marseille n’a pas de groupes de hooligans particulièrement connu, si il y’a émeute c’est plus fait par des random contre des hooligans d’autres endroits.
Voici ceux répertoriés par l’équipe
Forgot that inside the icon there's still a young girl from
Quelle vie terrible
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
@2sur10 ?
Si je prends un segment de taille pi par exemple, on est d'accord qu'il n'y pas de milieu a ce segment ? on peut s'en rapprocher infiniment mais on le sera jamais ? j'ai un collegue qui comprend pas ça me casse les couilles je sais pas comment lui expliquer
Si je prends un segment de taille pi par exemple, on est d'accord qu'il n'y pas de milieu a ce segment ? on peut s'en rapprocher infiniment mais on le sera jamais ? j'ai un collegue qui comprend pas ça me casse les couilles je sais pas comment lui expliquer
Bah le milieu c'est le point à distance pi/2 des extrémités, bien sûr qu'il existe (si l'espace a les bonnes propriétés de complétude)
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Oh non c’est une réaction assez commune de baisse d’adrénaline ( à potentiel très haut en regardant un match où son équipe joue ) mêlée à une grosse frustration. Chaque gros supporter de n’importe quel sport pourrait le ressentir
Justement ce que je déplore c’est le côté animal de certains, comment un adulte sain et bien portant n’arrive pas à gérer sa frustration au point de vouloir tirer sur ses adversaires après un match
Justement ce que je déplore c’est le côté animal de certains, comment un adulte sain et bien portant n’arrive pas à gérer sa frustration au point de vouloir tirer sur ses adversaires après un match
Forgot that inside the icon there's still a young girl from
Mais pourquoi trainais tu avec eux surtout
Forgot that inside the icon there's still a young girl from
tu veux ? . . .
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Ça parle de lyon ici hey pelo 69 la trick tu connais on aime écouter de la funk dans le bat’ et manger des tacos 
Chaîne youtube aux vidéos effrayantes https://youtube.com/@reve[...]t3110?si=DrDCiPpZTQq6hDwx
@2sur10 ?
Si je prends un segment de taille pi par exemple, on est d'accord qu'il n'y pas de milieu a ce segment ? on peut s'en rapprocher infiniment mais on le sera jamais ? j'ai un collegue qui comprend pas ça me casse les couilles je sais pas comment lui expliquer
Si je prends un segment de taille pi par exemple, on est d'accord qu'il n'y pas de milieu a ce segment ? on peut s'en rapprocher infiniment mais on le sera jamais ? j'ai un collegue qui comprend pas ça me casse les couilles je sais pas comment lui expliquer
π est un nombre irrationnel donc on ne peut pas raisonner de la même façon qu’avec des nombres rationnels
Le milieu du segment est π/2, ce milieu existe
Mais toi, humble mortel, qui évolue dans un monde rationnel et fini, tu ne pourras jamais avoir un segment physique de longueur π ni même pointer son milieu avec ton petit doigt
Le milieu du segment est π/2, ce milieu existe
Mais toi, humble mortel, qui évolue dans un monde rationnel et fini, tu ne pourras jamais avoir un segment physique de longueur π ni même pointer son milieu avec ton petit doigt
Forgot that inside the icon there's still a young girl from
Un 1v1 sur WS
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Bah le milieu c'est le point à distance pi/2 des extrémités, bien sûr qu'il existe (si l'espace a les bonnes propriétés de complétude)
En gros la question c'est plutot, que tu peux pas trouver retionnel en divisant par 2 un chiffre irrationnel
Mais c'etait très mal formuler, et on s'est comprit avec mon ocllegue du coup
Mais c'etait très mal formuler, et on s'est comprit avec mon ocllegue du coup
Règle ->
Bloqué à l'age de fer
Map gigantesque
Animaux sauvage doublés
Bloqué à l'age de fer
Map gigantesque
Animaux sauvage doublés
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Ah bah je pensais avoir compris mais du coup non, j'arrive effectivement pas a imaginer le milieu d'un nombre infini
On commence quand du coup?
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
Ah bah je pensais avoir compris mais du coup non, j'arrive effectivement pas a imaginer le milieu d'un nombre infini
Avant d’imaginer le milieu, arrives tu à imaginer le segment ?
Genre une corde qui n’est pas plus grande que 4cm mais qui pourtant ne se finit jamais
On ne peut pas, c’est un concept trop irrationnel pour nos petits cerveaux
Genre une corde qui n’est pas plus grande que 4cm mais qui pourtant ne se finit jamais
On ne peut pas, c’est un concept trop irrationnel pour nos petits cerveaux
Forgot that inside the icon there's still a young girl from
Avant d’imaginer le milieu, arrives tu à imaginer le segment ?
Genre une corde qui n’est pas plus grande que 4cm mais qui pourtant ne se finit jamais
On ne peut pas, c’est un concept trop irrationnel pour nos petits cerveaux
Genre une corde qui n’est pas plus grande que 4cm mais qui pourtant ne se finit jamais
On ne peut pas, c’est un concept trop irrationnel pour nos petits cerveaux
Bah après 4cm y'a plus de corde, alors infinie laisse moi rire
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.
De rien les matheux rappelez moi quand vous avez besoin
Gardez mémoire de moi, non point tel que j’ai failli, mais tel que j’étais.