Bonjour, petit topic pour répondre à la question d'un khey ( @Kikuta ) sur ce qu'est l'entropie.
Comme ma réponse commençait à être longue, j'en fais un topic, peut être que ça intéresse d'autres personnes ?
En physique, lorsqu'on étudie des systèmes complexes (comme un gaz), il est presque impossible d'écrire et de résoudre les équations de Newton pour chacune d'elles. Alors plutôt que d'analyser individuellement chaque particule, on adopte une approche statistique, en décrivant le système à l’aide de probabilités définies sur l’ensemble des états possibles.
Pour ça, on utilise la fonction de partition Z, qui compte et pondère tous les états accessibles du système. Cette fonction permet de retrouver toutes les grandeurs thermodynamiques essentielles du système (y compris l'énergie, l'entropie et les potentiels thermodynamiques).
Voici quelques façons de voir ce qu’est l'entropie à partir des configurations du système (c-à-d à partir de Z, ou grand oméga dans la définition de bolzmann)
La définition officielle (boltzmann), si on étudie un système avec une énergie totale fixée:
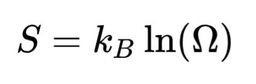
Ou encore, si on choisi d’avoir notre système qui échange de l’énergie avec un réservoir:
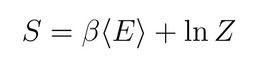
Ainsi, l’entropie découle directement de Z, et donc des configurations microscopiques du système étudié. Plus un système a de façons d’exister, plus son entropie sera grande.
Un exemple pour avoir un peu plus d’intuition sur les états disponibles:
Les molécules d’eau d’un glaçon dans un verre ont une structure bien ordonnée. Il y a peu de configuration possibles dans l’espace des phases (globalement les molécules ne bougent pas et restent au même endroit) : faible entropie.
Lorsque le glaçon fond, les molécules d’eau deviennent plus libres et désordonnées. Les molécules peuvent partir dans toutes les directions et avec des vitesses variées, ce qui augmente le nombre de configurations possibles dans l’espace des phases : augmentation de l’entropie.
DOU YOU NOW POMER L'EAU
YOU GO TO POMER L'EAU
(D’ailleurs c ’est une illustration du second principe de la thermodynamique : l’entropie d’un système isolé tend à augmenter)
Et là, on peut se dire:
“Oui mais, PiedJuteux, tu as dis que la fonction de partition Z permet de retrouver toutes tes grandeurs thermodynamiques. On a donc accès à l'énergie et tout le reste, pourquoi s’intéresser alors à l’entropie ?” -> -> ->
La fonction de partition Z est effectivement très utile, mais l’entropie ajoute une information cruciale : la répartition des états et la direction d’évolution du système (expliquant d’ailleurs pourquoi certains processus sont irréversibles). Grâce à l’entropie, que l'on peut retrouver à partir de Z donc, il est possible de :
- prédire l’équilibre du système (sans suivre chaque particule avec les equations de Newton)
- dériver des équations d’état
- décrire les transitions de phase (comme la fusion ou l’évaporation)
- comprendre la perte ou la transmission d’information dans un système physique
On peut aussi utiliser l’entropie pour optimiser les rendements des machines thermiques en comprenant où se produisent les pertes énergétiques. Mais ça fait très longtemps que je n’ai pas revu ça en détail donc je vais omettre toutes la partie sur les machines thermiques
Sinon, une autre façon de développer une intuition sur l’entropie est de regarder cette équation:
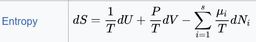
Augmentation d’énergie interne U (avec V et N fixés) -> augmentation de l’entropie S
Augmentation du volume V (avec U et N fixés) -> augmentation de S
Augmentation du nombre total de particules N (avec V et U fixés) -> diminution de l’entropie (à cause du plus grand nombre de particules, il y a moins de configurations possible dans notre système)
Comme ma réponse commençait à être longue, j'en fais un topic, peut être que ça intéresse d'autres personnes ?
Pour ça, on utilise la fonction de partition Z, qui compte et pondère tous les états accessibles du système. Cette fonction permet de retrouver toutes les grandeurs thermodynamiques essentielles du système (y compris l'énergie, l'entropie et les potentiels thermodynamiques).
Voici quelques façons de voir ce qu’est l'entropie à partir des configurations du système (c-à-d à partir de Z, ou grand oméga dans la définition de bolzmann)
La définition officielle (boltzmann), si on étudie un système avec une énergie totale fixée:
Ou encore, si on choisi d’avoir notre système qui échange de l’énergie avec un réservoir:
Le développement, si besoin: 
Les molécules d’eau d’un glaçon dans un verre ont une structure bien ordonnée. Il y a peu de configuration possibles dans l’espace des phases (globalement les molécules ne bougent pas et restent au même endroit) : faible entropie.
Lorsque le glaçon fond, les molécules d’eau deviennent plus libres et désordonnées. Les molécules peuvent partir dans toutes les directions et avec des vitesses variées, ce qui augmente le nombre de configurations possibles dans l’espace des phases : augmentation de l’entropie.
(D’ailleurs c ’est une illustration du second principe de la thermodynamique : l’entropie d’un système isolé tend à augmenter)
Et là, on peut se dire:
- prédire l’équilibre du système (sans suivre chaque particule avec les equations de Newton)
- dériver des équations d’état
- décrire les transitions de phase (comme la fusion ou l’évaporation)
- comprendre la perte ou la transmission d’information dans un système physique
On peut aussi utiliser l’entropie pour optimiser les rendements des machines thermiques en comprenant où se produisent les pertes énergétiques. Mais ça fait très longtemps que je n’ai pas revu ça en détail donc je vais omettre toutes la partie sur les machines thermiques
Augmentation d’énergie interne U (avec V et N fixés) -> augmentation de l’entropie S
Augmentation du volume V (avec U et N fixés) -> augmentation de S
Augmentation du nombre total de particules N (avec V et U fixés) -> diminution de l’entropie (à cause du plus grand nombre de particules, il y a moins de configurations possible dans notre système)
Concrètement, voici quelques exemples d’utilisation de l’entropie dans certains exercices. Peut être que ça t’aideras à développer une intuition:
exemple 1, thermodynamique simple:
exemple 2, système de spins et matériaux: pour le modèle de spins de Curie-Weiss (utile pour étudier les propriétés magnétiques de certains matériaux):
exemple 3, retrouver des données correctes lorsque l'on mesure des données corrompues avec un bruit dont on peut modeler la loi de probabilité (ici on choisi un bruit gaussien):
exemple 1, thermodynamique simple:
Deux blocs à températures T1 et T2 qui sont collés, l’entropie montre qu’à l’équilibre les deux blocs auront la même température (ce qui maximize l’entropie). C’est un exemple trivial, tu peux trouver les développement sur internet.
exemple 2, système de spins et matériaux: pour le modèle de spins de Curie-Weiss (utile pour étudier les propriétés magnétiques de certains matériaux):
En maximisant l’entropie (ici notée f, bon c’est l’entropie libre ce qui n’est pas tout à fait pareil, mais équivalent):
On peut dériver une équation d’état qui caractérise notre système:
Et on peut observer à partir de quelle température (T), et quelle valeur de champ magnétique extérieur (Delta) le système de spin changera de phase (ferromagnétique ou paramagnétique: matériau aimanté ou non aimanté en gros). Il est possible de tracer notre fonction d’entropie, et de regarder quelles sont les valeurs qui la maximise, et comment ces valeurs des maximums évoluent lorsque l'on change la température et le champ magnétique externe (cela donne une intuition sur des transitions de phases du 1er ordre ou 2nd ordre)
Et bien sûr, à la fin on obtient un diagramme de phases:
Ce type d’exercice peut aider à caractériser les transition de phases dans les aimants par exemple, et pourquoi quand on chauffe un aimant au dessus d’un certain seuil (température de curie) cela détruit ses propriétés magnétiques.
exemple 3, retrouver des données correctes lorsque l'on mesure des données corrompues avec un bruit dont on peut modeler la loi de probabilité (ici on choisi un bruit gaussien):
Ici on étudie un tenseur 3D, mais on peut aussi imaginer la même chose en 2D (juste une matrice de données, comme une image qui est en mauvaise résolution, et que l'on souhaite récupérer en bonne qualité). On souhaite savoir à partir de quel taux de bruit (ou de corruption sur notre image) on peut récupérer une bonne image.
Comme avant, on calcule Z et dérive la fonction d’entropie (ici entropie libre notée phi):
Si on connait la distribution de notre bruit (ici on suppose gaussien), il est possible d'obtenir une expression plus simple, que l'on maximise pour ensuite trouver l’équation d’état du système:
Et encore une fois, on peut obtenir des diagrammes de phases sympathiques:
Note de fin:
Comment définir l’énergie en fonction de l’entropie ? On se doute bien que de l’eau fondue à une température de 0 degré à une énergie supérieure à cette même quantité d’eau solide à 0 degré, puisqu’il a bien fallu apporter de la chaleur pour faire fondre le glaçon. À la fin l’eau à la même température, mais pas la même énergie. Il faut en tenir compte lorsque l’on défini l’énergie en thermodynamique.
Ainsi, l’énergie du système dépend de l'entropie.
Maintenant, dans le réel, comment mesurer l’énergie du système puisque pour la définir on doit mesurer l’entropie ? (quantité qui ne se mesure pas lors d'une expérience en laboratoire).
Pour cela on utilise des quantités équivalentes à l'énergie (que l’on obtient grâce à des relations thermodynamiques et une transformée de legendre). Suivant les systèmes que l'on étudie et les quantité physiques mesurées, il est possible de calculer l’energie libre ou l’enthalpie ou l’enthalpie libre.
Ainsi, par exemple pour caractériser l’énergie de son système, un chimiste va calculer l’enthalpie libre (potentiel de Gibbs, une formulation de l’énergie qui ne dépend que de la température, pression et du nombres de particules). Ce potentiel de Gibbs est très utile pour étudier les réactions qui se produisent dans les conditions ambiantes de température et de pression.
Conclusion:
L’entropie est assez utile pour résoudre tout plein de types de problèmes, et est à la base du formalisme de la thermodynamique. J’ai toujours du mal à expliquer ce que c’est, j’espère avoir pu un peu donner quelques pistes. Globalement je considère ça comme une quantité physique un peu abstraite qui donne un ensemble de relations utiles sur le système, et aide à mieux le caractériser physiquement (un peu comme la température, la pression, etc nous donneront des informations sur ce qu’il se passe).
Ainsi, l’énergie du système dépend de l'entropie.
Maintenant, dans le réel, comment mesurer l’énergie du système puisque pour la définir on doit mesurer l’entropie ? (quantité qui ne se mesure pas lors d'une expérience en laboratoire).
Pour cela on utilise des quantités équivalentes à l'énergie (que l’on obtient grâce à des relations thermodynamiques et une transformée de legendre). Suivant les systèmes que l'on étudie et les quantité physiques mesurées, il est possible de calculer l’energie libre ou l’enthalpie ou l’enthalpie libre.
Ainsi, par exemple pour caractériser l’énergie de son système, un chimiste va calculer l’enthalpie libre (potentiel de Gibbs, une formulation de l’énergie qui ne dépend que de la température, pression et du nombres de particules). Ce potentiel de Gibbs est très utile pour étudier les réactions qui se produisent dans les conditions ambiantes de température et de pression.
L’entropie est assez utile pour résoudre tout plein de types de problèmes, et est à la base du formalisme de la thermodynamique. J’ai toujours du mal à expliquer ce que c’est, j’espère avoir pu un peu donner quelques pistes. Globalement je considère ça comme une quantité physique un peu abstraite qui donne un ensemble de relations utiles sur le système, et aide à mieux le caractériser physiquement (un peu comme la température, la pression, etc nous donneront des informations sur ce qu’il se passe).
Ayaaa, ce pseudo
Ayaaa, ce pseudo
up du soir
excellent topic
en espérant avoir pu éclairer certains points d'ombre dans ta compréhension de l'entropie
Concrètement, voici quelques exemples d’utilisation de l’entropie dans certains exercices. Peut être que ça t’aideras à développer une intuition:
exemple 1, thermodynamique simple:
exemple 2, système de spins et matériaux: pour le modèle de spins de Curie-Weiss (utile pour étudier les propriétés magnétiques de certains matériaux):
exemple 3, retrouver des données correctes lorsque l'on mesure des données corrompues avec un bruit dont on peut modeler la loi de probabilité (ici on choisi un bruit gaussien):
exemple 1, thermodynamique simple:
Deux blocs à températures T1 et T2 qui sont collés, l’entropie montre qu’à l’équilibre les deux blocs auront la même température (ce qui maximize l’entropie). C’est un exemple trivial, tu peux trouver les développement sur internet.
exemple 2, système de spins et matériaux: pour le modèle de spins de Curie-Weiss (utile pour étudier les propriétés magnétiques de certains matériaux):
En maximisant l’entropie (ici notée f, bon c’est l’entropie libre ce qui n’est pas tout à fait pareil, mais équivalent):
On peut dériver une équation d’état qui caractérise notre système:
Et on peut observer à partir de quelle température (T), et quelle valeur de champ magnétique extérieur (Delta) le système de spin changera de phase (ferromagnétique ou paramagnétique: matériau aimanté ou non aimanté en gros). Il est possible de tracer notre fonction d’entropie, et de regarder quelles sont les valeurs qui la maximise, et comment ces valeurs des maximums évoluent lorsque l'on change la température et le champ magnétique externe (cela donne une intuition sur des transitions de phases du 1er ordre ou 2nd ordre)
Et bien sûr, à la fin on obtient un diagramme de phases:
Ce type d’exercice peut aider à caractériser les transition de phases dans les aimants par exemple, et pourquoi quand on chauffe un aimant au dessus d’un certain seuil (température de curie) cela détruit ses propriétés magnétiques.
exemple 3, retrouver des données correctes lorsque l'on mesure des données corrompues avec un bruit dont on peut modeler la loi de probabilité (ici on choisi un bruit gaussien):
Ici on étudie un tenseur 3D, mais on peut aussi imaginer la même chose en 2D (juste une matrice de données, comme une image qui est en mauvaise résolution, et que l'on souhaite récupérer en bonne qualité). On souhaite savoir à partir de quel taux de bruit (ou de corruption sur notre image) on peut récupérer une bonne image.
Comme avant, on calcule Z et dérive la fonction d’entropie (ici entropie libre notée phi):
Si on connait la distribution de notre bruit (ici on suppose gaussien), il est possible d'obtenir une expression plus simple, que l'on maximise pour ensuite trouver l’équation d’état du système:
Et encore une fois, on peut obtenir des diagrammes de phases sympathiques:
Ayaaa c'est tellement trivial
Non, dans mon exercice on supposait que notre tenseur (ou notre image) était dégradée par un bruit gaussien pour calculer l'entropie.
Après ce n'est pas forcément le cas dans la vraie vie, ça aurait pu être une autre distribution (continue, laplace, etc).
Après c'est vraiment un domaine niche et assez récent de la physique statistique, très théorique
Par contre, cette méthode ne se base pas sur l'AI. Ni sur des convolutions. Mais plutôt sur la formule de bayes que tu utilises pour déterminer un estimateur pour ton image d'origine (estimateur qui maximise l'entropie).
La convolution ça semble être pour améliorer une image floutée, là c'est pour améliorer une image corrompue avec du bruit, pas une image floue.
Bon après en pratique, pour obtenir concrètement ton estimateur tu peux utiliser des méthodes de montée de gradient (un peu comme en ml quand tu fais des descentes de gradient). Mais c'est fondamentalement différent des encodeur-décodeurs que tu utilises pour débruiter les images avec l'AI.
Voici quelques exemples :
Après ce n'est pas forcément le cas dans la vraie vie, ça aurait pu être une autre distribution (continue, laplace, etc).
Exemple: tu utilises une machine pour faire des mesures. Cette machine fait des erreurs de mesure (et donc il y a du bruit). Tu peux alors faire des tests et déterminer la loi de probabilité de ton bruit. Et à la fin quand tu feras de nouvelles mesures, tu pourras "supprimer" dans une certaine limite le bruit, grâce à la méthode de maximisation de l'entropie que j'ai présenté dans le topic.
(il faut juste remplacer la distribution gaussienne que j'ai utilisée dans les calculs par la distribution de l'erreur de ta machine).
Après c'est vraiment un domaine niche et assez récent de la physique statistique, très théorique
Par contre, cette méthode ne se base pas sur l'AI. Ni sur des convolutions. Mais plutôt sur la formule de bayes que tu utilises pour déterminer un estimateur pour ton image d'origine (estimateur qui maximise l'entropie).
La convolution ça semble être pour améliorer une image floutée, là c'est pour améliorer une image corrompue avec du bruit, pas une image floue.
Bon après en pratique, pour obtenir concrètement ton estimateur tu peux utiliser des méthodes de montée de gradient (un peu comme en ml quand tu fais des descentes de gradient). Mais c'est fondamentalement différent des encodeur-décodeurs que tu utilises pour débruiter les images avec l'AI.
Voici quelques exemples :
Chapitre 6 de ce pdf de Nishimori 
https://cdn.preterhuman.n[...]%20-%20Nishimori%20H..pdf
Non, dans mon exercice on supposait que notre tenseur (ou notre image) était dégradée par un bruit gaussien pour calculer l'entropie.
Après ce n'est pas forcément le cas dans la vraie vie, ça aurait pu être une autre distribution (continue, laplace, etc).
Après c'est vraiment un domaine niche et assez récent de la physique statistique, très théorique
Par contre, cette méthode ne se base pas sur l'AI. Ni sur des convolutions. Mais plutôt sur la formule de bayes que tu utilises pour déterminer un estimateur pour ton image d'origine (estimateur qui maximise l'entropie).
La convolution ça semble être pour améliorer une image floutée, là c'est pour améliorer une image corrompue avec du bruit, pas une image floue.
Bon après en pratique, pour obtenir concrètement ton estimateur tu peux utiliser des méthodes de montée de gradient (un peu comme en ml quand tu fais des descentes de gradient). Mais c'est fondamentalement différent des encodeur-décodeurs que tu utilises pour débruiter les images avec l'AI.
Voici quelques exemples :
Après ce n'est pas forcément le cas dans la vraie vie, ça aurait pu être une autre distribution (continue, laplace, etc).
Exemple: tu utilises une machine pour faire des mesures. Cette machine fait des erreurs de mesure (et donc il y a du bruit). Tu peux alors faire des tests et déterminer la loi de probabilité de ton bruit. Et à la fin quand tu feras de nouvelles mesures, tu pourras "supprimer" dans une certaine limite le bruit, grâce à la méthode de maximisation de l'entropie que j'ai présenté dans le topic.
(il faut juste remplacer la distribution gaussienne que j'ai utilisée dans les calculs par la distribution de l'erreur de ta machine).
Après c'est vraiment un domaine niche et assez récent de la physique statistique, très théorique
Par contre, cette méthode ne se base pas sur l'AI. Ni sur des convolutions. Mais plutôt sur la formule de bayes que tu utilises pour déterminer un estimateur pour ton image d'origine (estimateur qui maximise l'entropie).
La convolution ça semble être pour améliorer une image floutée, là c'est pour améliorer une image corrompue avec du bruit, pas une image floue.
Bon après en pratique, pour obtenir concrètement ton estimateur tu peux utiliser des méthodes de montée de gradient (un peu comme en ml quand tu fais des descentes de gradient). Mais c'est fondamentalement différent des encodeur-décodeurs que tu utilises pour débruiter les images avec l'AI.
Voici quelques exemples :
Chapitre 6 de ce pdf de Nishimori https://cdn.preterhuman.n[...]%20-%20Nishimori%20H..pdf
Bonjour, petit topic pour répondre à la question d'un khey ( @Kikuta ) sur ce qu'est l'entropie.
Comme ma réponse commençait à être longue, j'en fais un topic, peut être que ça intéresse d'autres personnes ?
En physique, lorsqu'on étudie des systèmes complexes (comme un gaz), il est presque impossible d'écrire et de résoudre les équations de Newton pour chacune d'elles. Alors plutôt que d'analyser individuellement chaque particule, on adopte une approche statistique, en décrivant le système à l’aide de probabilités définies sur l’ensemble des états possibles.
Pour ça, on utilise la fonction de partition Z, qui compte et pondère tous les états accessibles du système. Cette fonction permet de retrouver toutes les grandeurs thermodynamiques essentielles du système (y compris l'énergie, l'entropie et les potentiels thermodynamiques).
Voici quelques façons de voir ce qu’est l'entropie à partir des configurations du système (c-à-d à partir de Z, ou grand oméga dans la définition de bolzmann)
La définition officielle (boltzmann), si on étudie un système avec une énergie totale fixée:
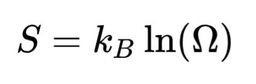
Ou encore, si on choisi d’avoir notre système qui échange de l’énergie avec un réservoir:
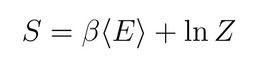
Ainsi, l’entropie découle directement de Z, et donc des configurations microscopiques du système étudié. Plus un système a de façons d’exister, plus son entropie sera grande.
Un exemple pour avoir un peu plus d’intuition sur les états disponibles:
Les molécules d’eau d’un glaçon dans un verre ont une structure bien ordonnée. Il y a peu de configuration possibles dans l’espace des phases (globalement les molécules ne bougent pas et restent au même endroit) : faible entropie.
Lorsque le glaçon fond, les molécules d’eau deviennent plus libres et désordonnées. Les molécules peuvent partir dans toutes les directions et avec des vitesses variées, ce qui augmente le nombre de configurations possibles dans l’espace des phases : augmentation de l’entropie.
DOU YOU NOW POMER L'EAU
YOU GO TO POMER L'EAU
(D’ailleurs c ’est une illustration du second principe de la thermodynamique : l’entropie d’un système isolé tend à augmenter)
Et là, on peut se dire:
“Oui mais, PiedJuteux, tu as dis que la fonction de partition Z permet de retrouver toutes tes grandeurs thermodynamiques. On a donc accès à l'énergie et tout le reste, pourquoi s’intéresser alors à l’entropie ?” -> -> ->
La fonction de partition Z est effectivement très utile, mais l’entropie ajoute une information cruciale : la répartition des états et la direction d’évolution du système (expliquant d’ailleurs pourquoi certains processus sont irréversibles). Grâce à l’entropie, que l'on peut retrouver à partir de Z donc, il est possible de :
- prédire l’équilibre du système (sans suivre chaque particule avec les equations de Newton)
- dériver des équations d’état
- décrire les transitions de phase (comme la fusion ou l’évaporation)
- comprendre la perte ou la transmission d’information dans un système physique
On peut aussi utiliser l’entropie pour optimiser les rendements des machines thermiques en comprenant où se produisent les pertes énergétiques. Mais ça fait très longtemps que je n’ai pas revu ça en détail donc je vais omettre toutes la partie sur les machines thermiques
Sinon, une autre façon de développer une intuition sur l’entropie est de regarder cette équation:
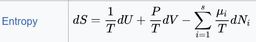
Augmentation d’énergie interne U (avec V et N fixés) -> augmentation de l’entropie S
Augmentation du volume V (avec U et N fixés) -> augmentation de S
Augmentation du nombre total de particules N (avec V et U fixés) -> diminution de l’entropie (à cause du plus grand nombre de particules, il y a moins de configurations possible dans notre système)
Comme ma réponse commençait à être longue, j'en fais un topic, peut être que ça intéresse d'autres personnes ?
Pour ça, on utilise la fonction de partition Z, qui compte et pondère tous les états accessibles du système. Cette fonction permet de retrouver toutes les grandeurs thermodynamiques essentielles du système (y compris l'énergie, l'entropie et les potentiels thermodynamiques).
Voici quelques façons de voir ce qu’est l'entropie à partir des configurations du système (c-à-d à partir de Z, ou grand oméga dans la définition de bolzmann)
La définition officielle (boltzmann), si on étudie un système avec une énergie totale fixée:
Ou encore, si on choisi d’avoir notre système qui échange de l’énergie avec un réservoir:
Le développement, si besoin:
Les molécules d’eau d’un glaçon dans un verre ont une structure bien ordonnée. Il y a peu de configuration possibles dans l’espace des phases (globalement les molécules ne bougent pas et restent au même endroit) : faible entropie.
Lorsque le glaçon fond, les molécules d’eau deviennent plus libres et désordonnées. Les molécules peuvent partir dans toutes les directions et avec des vitesses variées, ce qui augmente le nombre de configurations possibles dans l’espace des phases : augmentation de l’entropie.
(D’ailleurs c ’est une illustration du second principe de la thermodynamique : l’entropie d’un système isolé tend à augmenter)
Et là, on peut se dire:
- prédire l’équilibre du système (sans suivre chaque particule avec les equations de Newton)
- dériver des équations d’état
- décrire les transitions de phase (comme la fusion ou l’évaporation)
- comprendre la perte ou la transmission d’information dans un système physique
On peut aussi utiliser l’entropie pour optimiser les rendements des machines thermiques en comprenant où se produisent les pertes énergétiques. Mais ça fait très longtemps que je n’ai pas revu ça en détail donc je vais omettre toutes la partie sur les machines thermiques
Augmentation d’énergie interne U (avec V et N fixés) -> augmentation de l’entropie S
Augmentation du volume V (avec U et N fixés) -> augmentation de S
Augmentation du nombre total de particules N (avec V et U fixés) -> diminution de l’entropie (à cause du plus grand nombre de particules, il y a moins de configurations possible dans notre système)
J'ai une question
Si l'univers atteint son maximum d'entropie
qu'est ce qui n'empêche pas ensuite les particules à toutes converger vers le "centre" de l'univers sous l'effet de la gravitation ?
sachant que comme l'entropie est maximale, il n'y a donc pas d'énergie qui puisse s'opposer aux effets de la gravité
Si l'univers atteint son maximum d'entropie
qu'est ce qui n'empêche pas ensuite les particules à toutes converger vers le "centre" de l'univers sous l'effet de la gravitation ?
sachant que comme l'entropie est maximale, il n'y a donc pas d'énergie qui puisse s'opposer aux effets de la gravité
sinon ça va bien depuis l'IRL ?
