InscriptionConnexion
Yoneda
Yoneda
Élite double diamantComplotixTeam Chat
Mandrake
Mandrake
9 mois
euh, faut le scope sylphe pour résoudre ton problème je crois
:Bicyclette:
Le scope sylphe ?
:cat_think:
Vēritās līberābit vōs
il y a 9 mois
Mandrake
Mandrake
Jeune onchois de rang bronze
Image

:sueur2:
il y a 9 mois
Yoneda
Yoneda
Élite double diamantComplotixTeam Chat
Mace-Windu
Mace-Windu
9 mois
:rire:
au passage dans les espaces pointés t'as juste que Sigma est adjoint à gauche de Omega, mais c'est pas du tout une équivalence en général
:OuaisNanChaud:

une catégorie est stable précisément quand c'est une équivalence
:OuaisNanChaud:

enfin ça aurait pu être la déf
mais on a rajouté en plus "1 = 0" comme axiome (l'initial et le final c'est le même objet)
et là ça fait une catégorie "abélienne homotopique"
:chatfloreuh:
Vēritās līberābit vōs
il y a 9 mois
Yoneda
Yoneda
Élite double diamantComplotixTeam Chat
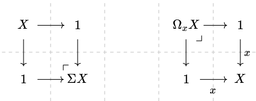
Ah au fait je parle de pullback et pushout au sens homotopique et non classique (c'est une def un peu différente, c'est dans des catégories de modèles, etc.)
Image
Vēritās līberābit vōs
il y a 9 mois
Yoneda
Yoneda
Élite double diamantComplotixTeam Chat
Yoneda
Yoneda
9 mois
au passage dans les espaces pointés t'as juste que Sigma est adjoint à gauche de Omega, mais c'est pas du tout une équivalence en général
:OuaisNanChaud:

une catégorie est stable précisément quand c'est une équivalence
:OuaisNanChaud:

enfin ça aurait pu être la déf
mais on a rajouté en plus "1 = 0" comme axiome (l'initial et le final c'est le même objet)
et là ça fait une catégorie "abélienne homotopique"
:chatfloreuh:
si tu veux une idée de preuve juste en utilisant le fait que c'est des pushout/pullback :

Hom(Sigma X,Y)
= Hom(1 U\_X 1,Y) (<- ici A U\_C B c'est une notation pour le pushout d'un diagramme A <- C -> B)
~ Hom(1,Y) U\_Hom(X,Y) Hom(1,Y) (<- où ici l'application Hom(X,Y) -> Hom(1,Y) au-dessus de laquelle on fait le pushout ça prend f : Hom(X,Y) et ça lui associe l'élément f(x) dans Y en gros, vu comme une application 1 -> Y)
~ Hom(X,Y ×\_1 Y) (<- tout pareil A ×\_C B c'est le pullback A <- C -> B)
= Hom(X,Omega Y)

si t'as jamais trop manipulé les limites/colimites en catégories la preuve est insuivable, il faudrait que j'explique plein de trucs mdr
Vēritās līberābit vōs
il y a 9 mois
hogankaple
hogankaple
Élite de rang diamantChef cuistoTeam ChatKikoojapNocturne
Yoneda
Yoneda
10 mois
Dans un spectre, la suite d'espaces pointés associée est générée par le smash produit avec S1 (S1 /\ X_n -> X_n+1) pour créer des suspensions itérés.
Ce genre de suite peut être vue comme une catégorie abelienne dans le sens où elle est suffisamment riche pour pouvoir faire de la cohomologie.

J'essaie de comprendre pourquoi le spectre de S est isomorphe à Z.
Comment identifie-t-on un spectre avec un groupe abelien ? Est-ce qu'on parle d'isormophisme parce que les groupes d'homotopies stables (qui sont eux bien des groupes abeliens) sur cette suite sont isomorphes à Z ?

Il y aurait l'idée que le spectre de S soit l'objet initial dans la catégorie des spectres de la même manière que Z l'est dans la catégorie des anneaux commutatifs.
ayaaaaa rien confruit
:Kj_bug_:
il y a 9 mois
Les sujets sont bon délire
Se connecter pour participer